Devlog
[백준 17472번] 다리 만들기 2 본문
17472번: 다리 만들기 2
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
www.acmicpc.net
이전 문제인 다리 만들기 1이 여러 개의 섬들 중, 두 개의 섬을 잇는 다리의 최소 길이를 구하는 문제였다면. 2탄은 모든 섬들을 잇는 다리 길이의 합의 최솟값을 구하는 문제입니다. 구현 폭탄에 그래프 종합 문제라 다리 만들기보다는 난이도가 더 높게 책정되어있긴 한데, 저한테는 1탄보다 2탄이 더 쉬웠습니다. 1탄을 아마 거의 1년 전에 풀었던 거 같은데, 그 당시 그래프 알고리즘은 커녕 DFS, BFS에서도 빌빌거렸던 시절이라 더 어려워 보였을 수도 있겠네요.
접근
MST(크루스칼 알고리즘, 분리 집합)
모든 섬을 잇는 다리들의 최소 값을 구해야 합니다.
너비 우선 탐색
다리들의 최솟값을 구하기 전에, 섬의 개수를 파악하고, 각 섬마다 번호를 붙여야 합니다.
브루트 포스 알고리즘
각 섬 사이의 간선들 중 최솟값을 구합니다. 다리 만들기 1을 푸신 분들도 알겠지만. BFS로 풀어야 할 걸 저는 브루트 포스로 풀었습니다. 그 이유는 다리 만들 때의 제약 조건에 있는데, 방향을 틀어도 되는 1탄과는 달리 2탄은 직선 형태의 다리를 만들어야 합니다. 이러한 제약 조건을 지킨 채 BFS를 돌리는 것은, 더 복잡한 구현을 요구하는 것으로 판단하여 모든 영역을 가로로 1번 완전탐색해서 가로 방향의 다리를 구하고, 세로로 1번 완전탐색해서 세로 방향의 다리를 구하는 것으로 구현했습니다.
시작하기 전에 풀어두면 좋은 문제들
BFS, 분리 집합, 크루스칼 알고리즘 이 세 개의 그래프 알고리즘을 이 하나의 문제에 전부 들이부어서 풀어야 하기 때문에 구현 난이도가 상당합니다. 그렇기 때문에 이 문제를 풀기 전에 미리 연습해두면 좋은 문제들을 아래에 모았습니다.
2667번: 단지번호붙이기
<그림 1>과 같이 정사각형 모양의 지도가 있다. 1은 집이 있는 곳을, 0은 집이 없는 곳을 나타낸다. 철수는 이 지도를 가지고 연결된 집의 모임인 단지를 정의하고, 단지에 번호를 붙이려 한다. 여
www.acmicpc.net
집이 모여있는 곳마다 단지 번호를 붙입니다. 인접해 있는 집끼리 동일한 번호를 붙인다는 점은, 각 섬마다 번호를 붙이는 것과 동일한 콘셉트입니다.
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
크루스칼 알고리즘 기본 문제입니다.
2146번: 다리 만들기
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다
www.acmicpc.net
다리 만들기 1탄으로 아까 위의 단자 번호 붙이기에 다리를 만드는 과정까지 추가되었습니다. 하지만 가장 짧은 다리 하나만 만들면 되는 문제로 너비 우선 탐색만 사용하면 됩니다.
알고리즘
섬에 번호 붙이기
인접 그래프로 주어졌습니다. 먼저 해야 할 일은 섬을 구별해야 합니다. 인접 행렬들을 전부 순회해서 값이 1이고 방문하지 않은 노드가 발견되면 그 자리에서 BFS를 수행하고 번호를 붙입니다. 번호는 2번부터 시작합니다.
label_offset = 1
island_size = 0
def in_range(i, j):
return (0 <= i < N) and (0 <= j < M)
# 라벨링
for i in range(N):
for j in range(M):
if G[i][j] == 1:
# 섬이지만 아직 방문을 하지 않은 경우 BFS 수행
island_size += 1
label = island_size + label_offset
Q = collections.deque([(i,j)])
G[i][j] = label
while Q:
si, sj = Q.pop()
for k in range(4):
ni, nj = si + di[k], sj + dj[k]
if not in_range(ni, nj) or G[ni][nj] != 1:
continue
G[ni][nj] = label # 값 1을 번호로 바꾸기
Q.appendleft((ni, nj))
WG = [[float('inf')] * (island_size+2) for _ in range(island_size+2)]간선 만들기
이게 간선을 만들어야 합니다. 요구하는 답도 모든 섬에 연결되어 있는 간선 길이의 합의 최솟값이므로 각 두 섬 사이의 간선을 만들 때, 가장 짧은 길이의 간선만 있어야 합니다. 그리고 이 간선은 한 뱡향으로만 향하는 직선이어야 합니다.
여기서 저는 BFS 알고리즘 대산 가로와 세로로 인접 그래프를 두 번 순회해서 간선들을 구했습니다.
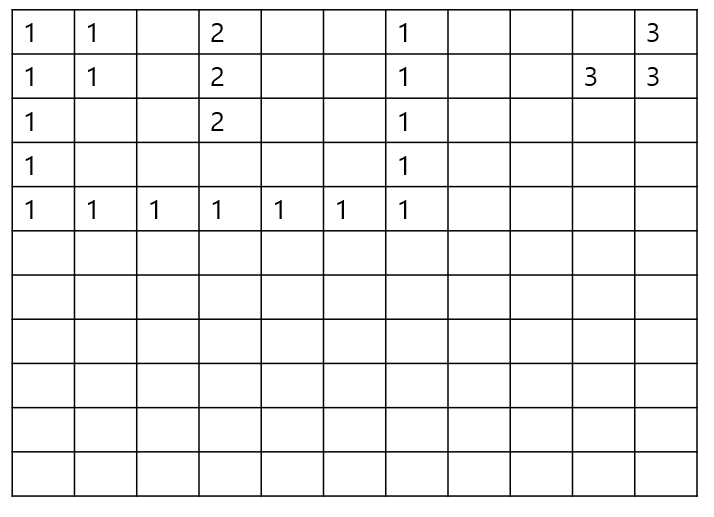
위와 같은 지도가 있다고 가정합니다.

1번 섬의 일부를 탐색했습니다. 다른 섬들과의 거리를 계산하기 위해 섬의 번호와 처음 발견한 위치를 저장합니다. 현재 저장된 정보는 [1, 0]입니다.

다시 같은 번호의 섬을 발견했습니다. 우리가 원하는 건 다리 즉, 간선의 최소 길이이므로 오른쪽에 있을수록 다른 섬과의 거리는 짧아집니다. 그러므로 저장되어 있던 위치 값 0을 1로 변경합니다. 이로써 저장된 정보는 [1, 0]에서 [1,1]으로 변경되었습니다.

비어있는 부분을 스킵하고 이번엔 2번을 만났습니다. 2번의 위치는 3입니다. 아까 저장된 위치는 1이므로 1번과 2번 사이의 다리 길이를 구할 수 있습니다. 두 섬 사이의 길이는 1이 되는데 길이가 2 이상일 경우만 다리를 만들 수 있기 때문에 이 경우는 제외합니다.
그리고 저장된 정보도 변경합니다. 2번 섬 위치에 있기 때문에 [1,1]에서 [2,3]으로 정보가 갱신됩니다.

하지만 1번 섬을 다시 발견했고 이번엔 길이가 2이기 때문에 다리를 세울 수 있습니다.

3번을 만났을 때도 동일한 방식으로 진행합니다.

두 번째 줄에서는 더 짧은 1과 3 사이의 거리가 발견되었습니다. 따라서 값을 3에서 2로 갱신합니다.
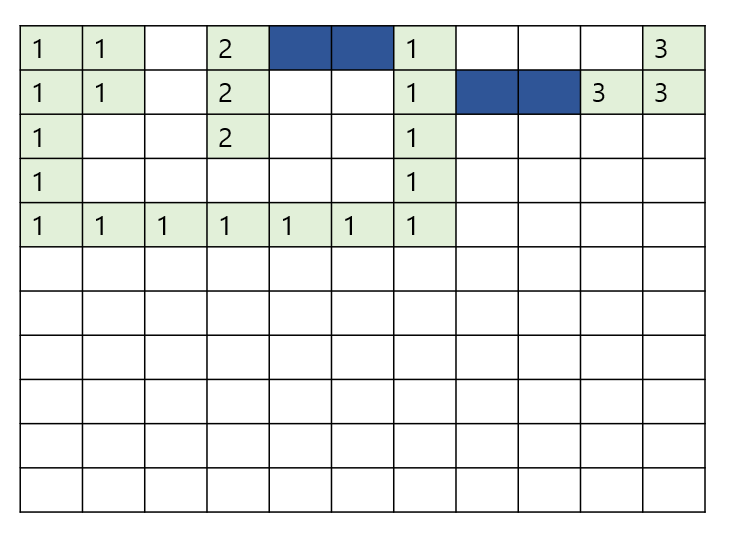
이 방식을 순회가 끝날 때까지 반복하면 짧은 길이의 간선들만 구할 수 있게 됩니다. 세로로 탐색하는 경우도 동일하게 진행합니다.
# 가로 다리 탐색
for i in range(N):
tmp_j, tmp_v = -1, -1
for j in range(M):
v = G[i][j]
if v > 0:
if tmp_v != v and tmp_j != -1:
w = j - tmp_j - 1
if w >= 2:
u = tmp_v
WG[u][v] = min(WG[u][v], w)
WG[v][u] = min(WG[v][u], w)
tmp_j, tmp_v = j, v
# 세로 다리 탐색
for j in range(M):
tmp_i, tmp_v = -1, -1
for i in range(N):
v = G[i][j]
if v > 0:
if tmp_v != v and tmp_i != -1:
w = i - tmp_i - 1
if w >= 2:
u = tmp_v
WG[u][v] = min(WG[u][v], w)
WG[v][u] = min(WG[v][u], w)
tmp_i, tmp_v = i, vu, v 사이의 짧은 간선을 저장하는 WG는 L(섬 개수) xL 형태의 2중 배열입니다. 크루스칼을 돌리려면 우선순위 큐 형태로 만들어야 하기 때문에 'inf'가 아닌 값들만 찾아서 우선순위 큐에 추가합니다.
E = []
# 간선 모으기
for u in range(2, island_size + 2):
for v in range(u, island_size + 2):
if WG[u][v] != float('inf'):
heapq.heappush(E, (WG[u][v], u, v))간선 연결하기
여기까지 왔다면 이제 간선 연결하는 일만 남았습니다. 간선도 전부 준비가 되어있기 때문에 MST 기본 문제 마냥 크루스칼 알고리즘을 돌리면 됩니다. 이렇게 해서 정답을 구할 수 있습니다.
전체 코드
import sys
import collections
import heapq
input = sys.stdin.readline
di, dj = [1,-1,0,0], [0,0,1,-1]
N, M = map(int, input()[:-1].split())
G = [list(map(int, input()[:-1].split())) for _ in range(N)]
label_offset = 1
island_size = 0
def in_range(i, j):
return (0 <= i < N) and (0 <= j < M)
# 라벨링
for i in range(N):
for j in range(M):
if G[i][j] == 1:
# 섬이지만 아직 방문을 하지 않은 경우 BFS 수행
island_size += 1
label = island_size + label_offset
Q = collections.deque([(i,j)])
G[i][j] = label
while Q:
si, sj = Q.pop()
for k in range(4):
ni, nj = si + di[k], sj + dj[k]
if not in_range(ni, nj) or G[ni][nj] != 1:
continue
G[ni][nj] = label # 값 1을 번호로 바꾸기
Q.appendleft((ni, nj))
WG = [[float('inf')] * (island_size+2) for _ in range(island_size+2)]
# 가로 다리 탐색
for i in range(N):
tmp_j, tmp_v = -1, -1
for j in range(M):
v = G[i][j]
if v > 0:
if tmp_v != v and tmp_j != -1:
w = j - tmp_j - 1
if w >= 2:
u = tmp_v
WG[u][v] = min(WG[u][v], w)
WG[v][u] = min(WG[v][u], w)
tmp_j, tmp_v = j, v
# 세로 다리 탐색
for j in range(M):
tmp_i, tmp_v = -1, -1
for i in range(N):
v = G[i][j]
if v > 0:
if tmp_v != v and tmp_i != -1:
w = i - tmp_i - 1
if w >= 2:
u = tmp_v
WG[u][v] = min(WG[u][v], w)
WG[v][u] = min(WG[v][u], w)
tmp_i, tmp_v = i, v
E = []
# 간선 모으기
for u in range(2, island_size + 2):
for v in range(u, island_size + 2):
if WG[u][v] != float('inf'):
heapq.heappush(E, (WG[u][v], u, v))
# 크루스칼 돌리기
parents = [i for i in range(island_size + 2)]
def find_parent(x):
if x == parents[x]:
return x
else:
parents[x] = find_parent(parents[x])
return parents[x]
def union_parent(a, b):
pa, pb = find_parent(a), find_parent(b)
if pa == pb:
return False
else:
if pa > pb:
parents[pb] = pa
else:
parents[pa] = pb
return True
edge_size = 0
ans = 0
while E and edge_size < (island_size - 1):
w, u, v = heapq.heappop(E)
if union_parent(u, v):
edge_size += 1
ans += w
if edge_size == island_size - 1:
print(ans)
else:
print(-1)
각종 그래프 알고리즘을 동원해서 푸는 문제이기 때문에 구현량이 상당합니다. 하지만 기본적인 사용법 정도만 요구하기 때문에, 문제의 요구사항을 잘 파악하고, 계획만 철저하게 세운다면 어렵지 않게 풀을 수 있습니다.
'Problem Solving > 코딩문제풀기' 카테고리의 다른 글
| [백준 1135] - 뉴스 전하기 (0) | 2022.06.16 |
|---|---|
| [백준 2631번] - 줄세우기 (0) | 2022.06.11 |
| 백준 - 나머지 합 (10986) (0) | 2022.05.17 |
| 백준 - Dance Dance Revolution (2342번) (0) | 2022.05.06 |
| 백준 - 비숍 (1799) (0) | 2022.05.05 |


