| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 데이터베이스
- 위상 정렬
- sqlalchemy
- Django
- 아파치
- 신입
- SQL
- 알고리즘
- flask
- 백준
- 리트코드
- 구성적
- MYSQL
- BFS
- FastAPI
- 백엔드
- scc
- 파이썬
- 강한 연결 요소
- alembic
- 취업
- 웹서버
- 테일러 급수
- 이분 탐색
- 수학
- 개발자
- api서버
- 가우스 소거법
- python
- C언어
- Today
- Total
Devlog
[백준 2133, 13976] 타일 채우기 1, 타일 채우기 2 본문
백준에서 타일 채우기 문제는 2개가 있습니다. 하나는 너비의 범위가 30 이하이고 다른 하나는 10^18입니다.
1탄
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
N = 2일 때 깔 수 있는 타일의 형태를 그려봅시다.

접근
N = 2일 때 둘 수 있는 경우의 수는 총 3입니다.
이렇게 보면 N = 1일 때의 경우의 수는 존재하지 않습니다. 그 이유는 높이가 3이기 때문에 타일의 각도가 [세로, 가로], [가로, 세로] 혹은 [가로, 가로, 가로]입니다. N = 1에 맞게 깔려면 오직 세로 형태만 깔아야 하는데 이때 세로의 길이는 항상 짝수가 되므로 높이가 3인 경우에는 N = 1 형태로 깔 수가 없습니다.
결국 깔린 타일의 너비는 2의 배수, 즉, 짝수 형태가 되고 N이 홀수인 경우는 전부 0이 됩니다.
어떻게 보면 위의 세 개의 타일 모양은 타일을 조합해서 깔 수 있는 최소의 단위라고 볼 수 있습니다. 왜냐하면 이들은 너비가 2로 가장 짧은 타일이고 N이 2보다 클 때 이를 조합해서 경우의 수의 일부를 구할 수 있으니까요. 위 그림의 3개의 타일 조합들을 차례대로 [0, 1, 2]라고 부릅시다.
다음은 N = 4인 경우입니다. 이때의 케이스는 아래와 같습니다.
[0, 0], [0, 1], [0, 2]
[1. 0], [1, 1], [1. 2]
[2. 0], [2. 1], [2, 2]
[?], [?]
총 11가지가 나옵니다. 기존 3개는 N=4는 N=2인 타일의 두 개를 조합한 것과 같기 때문에 3*3으로 구할 수 있었습니다. 하지만 나머지 두개(?)는 N=2타일의 조합으로 깔 수 없는 케이스인데 이 경우는 다음과 같습니다.
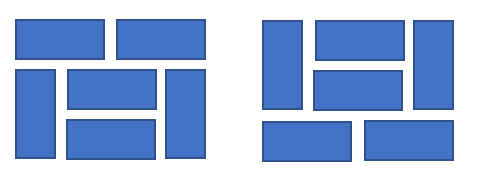
정중앙에 가로 형태의 타일을 두개 깔음으로써 N=2으로 조합이 불가능한 케이스를 메꿨습니다. 이 케이스들은 상하 대칭으로 총 2개가 됩니다. 따라서 N=4의 경우의 수는 3*3 + 2 = 11입니다. 이는 N=6 형태의 블록, N=8.... 인 경우에도 똑같이 경우의 수는 상하 대칭으로 2개가 됩니다. 그 이상을 고려하면 작은 타일 단위로 쪼개집니다.
N = 6일 때의 경우의 수를 알아봅시다.
N = 4였을 때처럼 단순히 N = 6이면 N=2가 세개니까 3*3*3에 2를 더해서 29인 것처럼 보이지만 하나가 빠졌습니다. 아까 N=4 경우의 수를 구했을 때 N=4 형태의 타일도 고려를 해야 합니다.
따라서 여기에서의 경우의 수를 구해보면 아래와 같습니다. 이때, 리스트의 요소는 0, 1, 2 같은 타일의 번호가 아니라 타일의 너비입니다.
[2, 2, 2] -> 3*3*3
[4, 2] -> 2*3
[2, 4] -> 3*2
[6] -> 2
차례대로 계산해 보면 27+6+6+2 = 41이 나옵니다. N=2 만의 조합 N=4, N=2 조합, N=6 조합을 전부 고려해서 계산했습니다.
하지만 이런 식의 계산은 고려해야 할 점이 너무 많습니다. 당장 N=8만 해도 [2,2,2,2]부터 시작해서 [4,2,2], [2,4,2], [6,2] 등... 케이스가 많아지고 N=30에서는 시간이 많이 걸릴지도 모릅니다. 특정 너비들의 타일 조합이 아니라 기존에 구했던 N=2, N=4일 때의 경우의 수 즉 이전 f(N)의 값들을 활용하는 방법 (다이나믹 프로그래밍)을 생각해 봐야 합니다.
점화식 유도
점화식 유도에 앞서 N값을 치환하려고 합니다.
n = N/2 (N이 짝수일 경우)
n는 N의 절반인 자연수로 정의했는데 그 이유는 어차피 N이 홀수인 경우는 0이기 때문에 이 경우는 아예 제외하려고 합니다.
다시 N=6일 때를 살펴봅시다.
[2, 2, 2] -> 3*3*3
[4, 2] -> 2*3
[2, 4] -> 3*2
[6] -> 2
N = n/2로 치환하면 아래와 같습니다.
[1, 1, 1] -> 3*3*3
[2, 1] -> 3*2
[1, 2] -> 2*3
[3] -> 2
그리고 얘들을 첫 번 째 요소의 기준으로 오름차순 정렬을 해 봅시다.
[1, 1, 1] -> 3*3*3
[1, 2] -> 3*2
[2, 1] -> 2*3
[3] -> 2
맨 앞의 요소 1과 매칭 되는 경우의 수는 [1,1], [2]입니다. 그런데 [1,1]과 [2]의 경우의 수를 합치면 3*3+2 = 11 f(2) 즉, N=4일 때의 경우의 수, f(2)가 됩니다. 2와 매칭되는 경우의 수 [1]도 f(1)이 되므로 f(3)을 다음과 같이 정리할 수 있습니다.
[1, f(2)] -> 3*11
[2, f(1)] -> 2*3
[3] -> 2
f(3) = 3*11 + 2*3 + 2 = 41
f(4) 즉 N=8인 경우도 쉽게 식을 세워서 구할 수 있습니다.
[1, f(3)] -> 3*41
[2, f(2)] -> 2*11
[3, f(1)] -> 2*3
[4] -> 2
f(4) = 123 + 22 + 6 + 2 = 153
이제 서서히 모양이 잡히기 시작합니다. 점화식을 구할 수 있을 것 같습니다. f(4)는
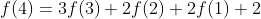
와 같고 f(n)으로 바꿔보면
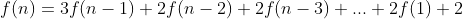
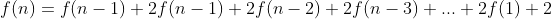
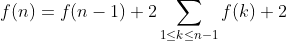
이 됩니다. (단, f(1)은 3입니다.) 점화식을 구했으니 바로 문제를 풀 수 있게 되었습니다.
import sys
input = sys.stdin.readline
N = int(input())
if N % 2 == 1:
print(0)
else:
n = N>>1
v = [0] * (n+1)
v[0] = 1
for k in range(1, n+1):
v[k] += v[k-1]
for i in range(1, k):
v[k] += (2*v[i])
v[k] += 2
print(v[n])점화식 최적화
시간 안에 통과되는 코드이지만. for k문에서 하나씩 돌 때마다 f(n-1)부터 f(1)의 합을 구하기 위해 또 반복문을 돌리기 때문에 O(n^2) 정도 걸립니다. 그냥 순수 f() 값들의 합을 요구하고 있기 때문에 누적합으로 바꿔버리면 그만입니다. 이제 시간 복잡도가 O(n)이 되었습니다.
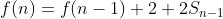
import sys
input = sys.stdin.readline
N = int(input())
if N % 2 == 1:
print(0)
else:
n = N>>1
s = [0] * (n+1)
v = [0] * (n+1)
s[1] = v[1] = 3
for k in range(2, n+1):
v[k] = v[k-1] + 2 + 2*s[k-1]
s[k] = s[k-1] + v[k]
print(v[n])
위는 O(n)이고 아래는 O(n^2)입니다. N의 범위가 작다 보니 눈에 띄지는 않지만. 조금이나마 개선이 되었습니다. 하지만 범위가 10^18인 2탄에서는 이런 방법 따위 얄짤없을뿐더러 미처 생각하지 못한 방식으로 풀어야 합니다.
2탄
13976번: 타일 채우기 2
첫째 줄에 N(1 ≤ N ≤ 1,000,000,000,000,000,000)이 주어진다.
www.acmicpc.net
O(n) 갖고는 풀 수 없습니다. 더 빠른 방법을 생각해 봐야 합니다. O(n) 보다 더 빠른 시간 복잡도라면 O(logn)이 있습니다.(여기서 밑은 2입니다.) O(n^(1/2))도 있긴 하지만 이거는 제가 잘 사용하지 않는 시간 복잡도라 잘 모르겠네요.
O(logn)이라면 대표적으로 분할 정복 또는, 재귀를 이용한 분할 거듭제곱이 있습니다. 분할 거듭제곱에 대해서 잘 모르시다면 아래의 문제를 푸는 것을 권장합니다.
1629번: 곱셈
첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.
www.acmicpc.net
코드 보기
import sys
input = sys.stdin.readline
def f(r, n, modula):
if n == 1:
return r % modula
else:
half = f(r, n>>1, modula)
res = (half * half) % modula
if n % 2: # 홀수
res = (res * f(r, 1, modula)) % modula
return res
a, b, c = map(int, input()[:-1].split())
print(f(a, b, c))
점화식 변형
일단 다시 만들었던 점화식을 봅시다.
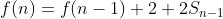
답도 없습니다. 제곱이 있는 것도 아니고 f(n-1)이 대놓고 앞에 있기 때문에 여기서 뭘 어떻게 할 수가 없습니다.
거듭제곱을 진행할 수 있도록 식을 어떻게든 유도해내야 합니다. 일단 f(n-1)를 좌변으로 옮겨 봅시다.
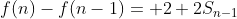
n를 n-1으로 바꿔봅니다.
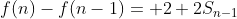
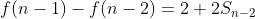
위 두식에 뺄셈을 진행하면 걸리적거리는 상수와 합을 없앨 수 있을 것 같습니다.
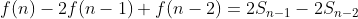
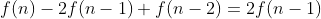
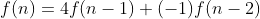
점화식이 어느 정도 간소화되었습니다. 상수화 합이 없어지고 함수만 남았습니다. 이래도 거듭제곱이 될만한 게 없어 보입니다.
4와 -1을 a와 b로 치환해 봅니다.
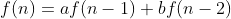
a = 1, b = 1을 하면
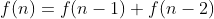
피보나치 수가 됩니다. 그리고 이 피보나치 수는 우리가 흔히 알고 있는 다이나믹 프로그래밍 말고도 행렬 거듭제곱으로 O(logn) 안에 풀 수 있는 방법이 있습니다.
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
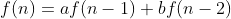
이 식이 있을 때
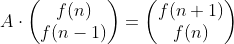
이 성립하는 행렬 A를 구해야 A행렬을 거듭제곱해서 빠른 시간 안에 값을 구할 수 있게 됩니다. 우변의 f(n+1)과 f(n)은 아래처럼
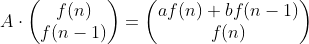
처럼 표현이 가능합니다.
일단 위의 f(n) -> af(n) + b(n-1)이 되려면 A의 1행은 a와 b가 되어야 합니다.
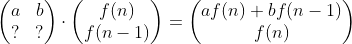
아래는 f(n-1) -> f(n)이 됩니다. f(n)을 1을 곱하고 f(n-1)을 0을 곱하기 때문에 아래와 같은 식이 됩니다.
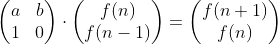
이렇게 A의 행렬을 구하게 되었습니다. 결국 f(n)에서 f(n+1)을 구하는 행렬 A는 위와 같고 f(n)에서 f(n+2)를 구하려면

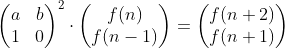
행렬 A를 제곱해서 f(n), f(n-1)과 곱하면 구할 수 있게 됩니다. 식을 일반화 하면
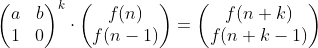
위와 같은 식이 됩니다. 이 공식은 피보나치 수 6과 타일 채우기 2 둘 다 적용이 가능하며 피보나치 공식은
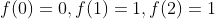
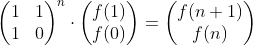
타일 채우기 2의 공식은
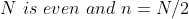
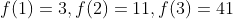
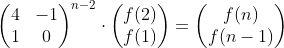
이렇게 됩니다. 위의 식을 토대로 코드를 작성하면 문제를 풀 수 있게 됩니다.
코드 보기 - 행렬 거듭제곱
행렬 거듭제곱의 메커니즘은 자연수 거듭제곱과 동일합니다. 단 곱셈 방식이 자연수에서 행렬로 바뀌었을 뿐입니다.
def mul(a, b):
return [
[
(a[0][0]*b[0][0] + a[0][1]*b[1][0]) % MODULA,
(a[0][0]*b[0][1] + a[0][1]*b[1][1]) % MODULA
],
[
(a[1][0]*b[0][0] + a[1][1]*b[1][0]) % MODULA,
(a[1][0]*b[0][1] + a[1][1]*b[1][1]) % MODULA
]
]
def f(n):
if n == 1:
return [
[4, -1],
[1, 0]
]
else:
half = f(n>>1)
res = mul(half, half)
if n & 0b1: # 홀수
res = mul(res, f(1))
return res백준에서도 행렬 거듭제곱에 관한 기본적인 문제가 있습니다. 풀어보시는 것을 권장합니다.
10830번: 행렬 제곱
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
코드 보기 - 전체
import sys
input = sys.stdin.readline
MODULA = 10**9 + 7
v = [1, 3, 11, 41]
def mul(a, b):
return [
[
(a[0][0]*b[0][0] + a[0][1]*b[1][0]) % MODULA,
(a[0][0]*b[0][1] + a[0][1]*b[1][1]) % MODULA
],
[
(a[1][0]*b[0][0] + a[1][1]*b[1][0]) % MODULA,
(a[1][0]*b[0][1] + a[1][1]*b[1][1]) % MODULA
]
]
def f(n):
if n == 1:
return [
[4, -1],
[1, 0]
]
else:
half = f(n>>1)
res = mul(half, half)
if n & 0b1: # 홀수
res = mul(res, f(1))
return res
n = int(input())
if n & 0b1:
print(0)
else:
n >>= 1
a = [
[v[2], v[1]],
[v[1], v[0]]
]
if n < 3:
print(v[n])
else:
ans = mul(f(n-2), a)
print(ans[0][0])참고
이렇게 점화식을 행렬로 푸는 방식을 행렬 멱법이라고 합니다. 다른 블로거 분께서 이해하기 쉽게 포스팅을 하셨습니다. 자세한 내용은 아래 링크를 참조하면 좋을 것 같습니다.
Matrix Exponentiation (행렬 멱법)
Matrix Exponentiation (행렬 멱법) Matrix Exponentiation 은 프로그래밍 문제 풀기에서 가장 많이 사용되는 기법입니다. 간단한 질문으로 Matrix Exponentiation 가 무엇인지 알아보겠습니다. $n$ 번째의 피보나..
zzonglove.tistory.com
끗

1탄에서 만든 점화식 들고 1시간 반 동안 신나게 요리하다가 겨우 f(n) = k*f(n-1) + p*f(n-2) 형태로 만들고 피보나치 거듭제곱이 생각나서 행렬로 풀을 수 있었습니다. 개인적으로 특정 알고리즘보다는 수식 세워서 푸는 것을 좋아하는 편이라 시간이 오래 걸렸어도 수식을 유도하고 풀이 방법을 찾는 과정이 나름 재밌었습니다.
'Problem Solving > 코딩문제풀기' 카테고리의 다른 글
| [백준 1039] 교환(Python) (0) | 2022.06.27 |
|---|---|
| [백준 1525] 퍼즐 (0) | 2022.06.21 |
| [백준 1135] - 뉴스 전하기 (0) | 2022.06.16 |
| [백준 2631번] - 줄세우기 (0) | 2022.06.11 |
| [백준 17472번] 다리 만들기 2 (0) | 2022.06.06 |



