| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 개발자
- alembic
- 데이터베이스
- 백엔드
- 구성적
- 위상 정렬
- FastAPI
- python
- C언어
- 강한 연결 요소
- 가우스 소거법
- sqlalchemy
- 이분 탐색
- 취업
- 테일러 급수
- 수학
- 알고리즘
- flask
- 웹서버
- api서버
- scc
- 파이썬
- Django
- 리트코드
- BFS
- MYSQL
- 백준
- 아파치
- 신입
- SQL
- Today
- Total
Devlog
[수치해석] 가우스 소거법으로 연립방정식을 풀어보자 본문
소개
중학교 수학에서 한번 씩 봤을 법한 연립방정식

이 문제를 푸는 방법은 2번 째 식에서 2를 곱해 2x + 2y = 6을 만든 다음 위의 식에 뺄셈을 진행하면 2y = 4가 되므로 y는 2가 됩니다. 그 다음 x +y = 3에 y = 2을 대입하면 x = 1이 되므로, 해는 x = 1, y = 2 이 됩니다.
이렇게 미지수가 두개인 경우, 둘 중 하나를 소거해서 다른 미지수의 해를 찾은 다음, 나머지 미지수의 해를 찾으면 됩니다. 그렇다면

미지수가 n개인 방정식 이 n개가 있는 연립 방정식. 이건 어떻게 풀어야 할까요? 가우스 소거법은 이렇게 무수히 많은 미지수와 방정식에 대한 풀이법을 알려줍니다!
종류
순수 가우스 소거법
피봇팅 가우스 소거법
가우스 조르단 소거법
피봇팅 가우스 조르단 소거법
대표적으로 가우스 소거법과 가우스-조르단 소거법이 있습니다. 하위 항목으로 다시 순수와 피봇팅으로 나뉘게 됩니다. 이번 포스트에서는 일반적인 가우스 소거법만 설명하려고 합니다. 왜냐하면 가우스-조르단 소거법은 역행렬을 구해서 연립방정식을 푸는 기법인데 이는 연립방정식 풀이 보다는 역행렬을 만드는 것에 가깝다고 판단하여 차후에 [선형대수학] 항목에서 역행렬과 함께 같이 다룰 예정입니다.
연립방정식을 행렬로 나타내기

가우스 소거법은 연립방정식을 행렬로 나타낸 다음 풀이를 진행합니다. 위의 연립방정식을 아래와 같이 행렬로 나타탤 수 있습니다.

일반화 하면 아래와 같은 식이 완성됩니다.

순수 가우스 소거법
원리
가우스 소거법의 원리는 맨 처음 미지수가 두 개인 연립방적식을 풀 때의 방식과 사실상 똑같습니다. 말 그대로 미지수를 왼쪽부터 하나 씩 지우면 됩니다.

이걸
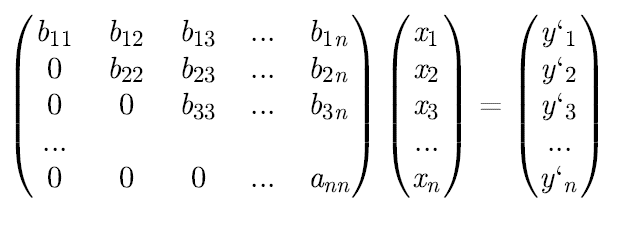
이렇게 사다리꼴 형태로 바꾸면 되는데, 이렇게 되면 맨 아랫줄에는 Xn의 계수만 남아있기 때문에 Xn을 구할 수 있게 되고 (보이지는 않지만)바로 위의 X(n-1)에서는 Xn는 이미 구했기 때문에 미지수는 X(n-1)만 남게 되어 X(n-1)의 값을 구할 수 있게 됩니다. 이렇게 하나 씩 올라가다 보면 X1의 값까지 구할 수 있게 됩니다.
풀이
예를 들어 아래와 같은 연립방정식이 있다고 가정해 봅시다.
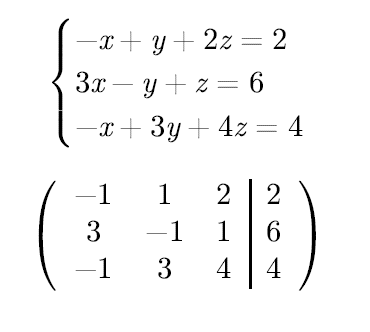
우선 2,3행의 x계수를 0으로 만들어야 합니다. 각 행과 1행의 x계수를 똑같이 맞춘 다음, 각 행에서 1행을 빼면 됩니다.

이렇게 해서 2,3행의 x계수를 0으로 맞췄습니다. 이번엔 y계수를 0으로 맞춰야 합니다. 아까와 똑같은 방법으로 진행합니다.

3행의 x,y 계수가 0이 되었습니다. 남는건 z, -5z=-10z이므로 z=2입니다.
2행의 2y+7z=12에서 z=2이므로 2y=-2, y=-1이 됩니다.
1행도 마찬가지로 -x+y+2z=2에서 y=-1,z=2이므로 -x-1+4=2, x=1입니다.
따라서 해는 x=1, y=-1, z=2 입니다.
코드(C++)
22940번: 선형 연립 방정식
하나 이상의 미지수에 대해 최고차항의 차수가 1을 넘지 않는 방정식을 선형 방정식이라 한다. 족, 다음과 같은 식을 의미한다. A1x1 + A2x2 + ... + Anxn = B 선형 연립 방정식이란 유한개의 선형 방
www.acmicpc.net
#include <iostream>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int N;
double matrix[6][7];
double ans[6];
cin >> N;
for(int i = 0; i < N; i++) {
for(int j = 0; j < N+1; j++)
cin >> matrix[i][j];
}
// 차례대로 계수 0으로 만들기
for(int k = 0; k < N-1; k++) {
for(int i = k+1; i < N; i++) {
double p = matrix[i][k] / matrix[k][k];
for(int j = k; j < N+1; j++) {
matrix[i][j] = matrix[i][j] - (matrix[k][j] * p);
}
}
}
// 맨 밑부터 시작해서 해 구하기
for(int i = N-1; i >= 0; i--) {
for(int j = N-1; j > i; j--)
matrix[i][N] -= (matrix[i][j] * ans[j]);
ans[i] = matrix[i][N] / matrix[i][i];
}
for(int i = 0; i < N; i++) cout << ans[i] << ' ';
cout << '\n';
return 0;
}피봇팅(pivoting) 가우스 소거법
순수 가우스 소거법에서는 맨 위의 행을 기준으로 잡고 아래의 행들의 계수를 0으로 맞춥니다. 그 과정에서 해당 행의 계수에 기준이 되는 행의 지우고자 하는 계수로 나누는 일이 생기게 되는데, 이때 기준의 되는 행의 계수가 0이 되면 0은 나눌 수 없는 수이므로 문제가 발생합니다. 이러한 상황을 방지하기 위해 0으로 만들기 전에, 행들 중 가장 계수의 절대값이 큰 행을 맨 위로 올려 놓고 이를 기준으로 잡고 진행하게 됩니다.

순수 가우스였다면 바로 0맞추기를 진행했겠지만, 우선 맨 위의 행을 계수가 가장 큰 행으로 바꿔야 합니다. 여기서는 3행의 계수가 |-2|로 가장 크기 때문에 1행과 3행을 맞바꿉니다.

그 다음 가우스 소거법을 수행합니다.
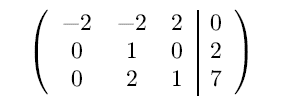
여기서 3행의 계수(2)가 2행(1)보다 더 크기 때문에 자리바꿈합니다.
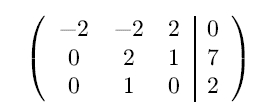
마찬가지로 가우스 소거법을 수행합니다.

이렇게 해서 모든 해들 구할 수 있게 되었고, 해는 z=3, y=2, x=1이 됩니다.
코드(C++)
알고리즘 자체는 변한 부분은 없고 계수를 0으로 만들기 전, 계수의 절댓값이 가장 큰 행과 맨 위의 행을 스왑하는 과정이 생겼습니다.
// 계수가 가장 큰 행을 메인으로 잡는다.
int pivot_i = k;
double tmp;
for(int i = k+1; i < N; i++)
if(abs(matrix[pivot_i][k]) < abs(matrix[i][k]))
pivot_i = i;
// 맨 위의 행과 자리바꿈한다.
for(int j = 0; j < N+1; j++)
{
tmp = matrix[k][j];
matrix[k][j] = matrix[pivot_i][j];
matrix[pivot_i][j] = tmp;
}
'수학 관련 > 수치해석' 카테고리의 다른 글
| [수치해석] 테일러 급수 (2) - 테일러 다항식과 테일러 다항식의 오차 구하기 (0) | 2022.07.14 |
|---|---|
| [수치해석] 테일러 급수 (1) - cos, sin, 제곱근 함수를 수학모듈 없이 직접 구현해 보자 (0) | 2022.07.11 |


