| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- MYSQL
- sqlalchemy
- Django
- 구성적
- alembic
- BFS
- FastAPI
- api서버
- 신입
- 테일러 급수
- 백준
- 아파치
- scc
- 파이썬
- 알고리즘
- 취업
- SQL
- 개발자
- flask
- python
- C언어
- 가우스 소거법
- 이분 탐색
- 데이터베이스
- 리트코드
- 웹서버
- 백엔드
- 수학
- 위상 정렬
- 강한 연결 요소
- Today
- Total
Devlog
[수치해석] 테일러 급수 (1) - cos, sin, 제곱근 함수를 수학모듈 없이 직접 구현해 보자 본문
테일러 급수 시리즈
1. 테일러 급수 전개하기
2. 테일러 다항식 오차 계산하기
소개
테일러 급수는 어떤 함수의 값(임의의 지점의 값)을 무한한 항의 합으로 나타내는 방법입니다. 즉, 함수를 다항식의 형태로 변환을 하는 방식이며 이때 근사값을 구할 수 있습니다. 테일러 급수를 사용하는 방법만 알면, 수학 모듈이 아니면 직접 구하기가 힘든 제곱근이나 삼각함수 등을 테일러 급수를 활용해 수학 관련 모듈 없이 직접 하드코딩 할 수 있습니다.
이 블로그에서의 테일러 급수 시리즈는 (1)테일러 급수 전개하기, (2)테일러 다항식 오차 계산하기 이렇게 두 챕터로 나눠서 진행합니다.
조건
하지만 모든 함수들을 테일러 급수로 나타낼 수 없습니다. 위의 공식에서 나타냈듯이, 미분을 사용하고 있기 때문에 임의의 지점에서 미분이 무한대로 가능해야 합니다. 무한대 까진 아니더라도 테일러 다항식의 항의 갯수 만큼 미분이 가능해야 합니다. 테일러 다항식은 다음 챕터에서 설명할 예정입니다.
증명
증명 과정은 위키백과를 참고했습니다.

모든 범위에서 전부 무한대로 미분 가능한 함수 f(x)가 있습니다.

미분이 가능하기 때문에 위와 같은 식도 가능합니다. (미적분학 제2 기본 정리) 이때 x와 a는 실수 범위의 수이고 a는 임의의 실수 입니다.

또한 아래처럼 표현이 가능합니다. 식을 우항처럼 작성한 이유는 (-1)과 (-f'(x))로 쪼개서 부분적분을 진행하려고 하기 때문입니다.

부분적분의 공식은 위와 같습니다. 보다시피 v'(x)는 적분용, u(x)는 미분용 입니다. v'(t) = (-1), u(t) = -f'(t)로 두고 부분적분을 진행해 봅시다.



위와 같은 식으로 변형이 되었습니다. -1를 적분하면 -t+C가 나오고 C는 임의의 상수 입니다. 이때 t를 중심으로 미/적분이 진행되고 있으므로 x를 상수로 잡을 수 있습니다. 따라서 -1의 적분을 -t+x로 잡습니다.
이렇게 되면 u(t)v(t)를 세 번 째 식처럼 간단하게 만들 수 있습니다.
오른쪽 항에 대해 부분적분을 다시 진행해 봅니다. 마찬가지로 v'(t) = -t+x, u(t) = -f''(t)로 잡고 진행합니다. 그런데 v'(t)을 적분한 v(t)를 구해보면

-1을 적분했을 때보다 조금 더 복잡한 식이 만들어 집니다. 일단 모든 항을 -1/2로 묶어 봅시다.
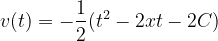
t^2의 계수가 1, t의 계수는 2x입니다. 그렇다면 2C를 x^2로 잡게 되면 완전제곱꼴로 만들 수 있습니다.
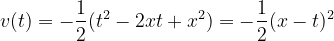
v(t)를 구했으니 부분적분을 진행해 봅니다.

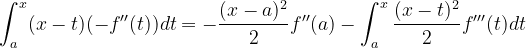
이제 기존의 식과 합치면

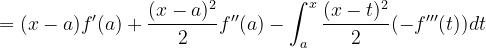
이제 모양이 보이기 시작합니다. 첫번 째 항 부터 순서대로 (x-a)의 거듭제곱과 f(x)의 미분을 계속 진행하고 있습니다. 오른족의 항을 계속 부분적분을 진행하게 되면
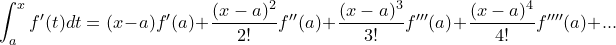
위와 같은 식이 완성되고 f'(t)의 x~a까지의 적분은 f(x) - f(a)로 나타낼 수 있기 때문에 -f(a)을 우변으로 보내면 아래처럼 f(x)의 테일러 급수가 완성이 됩니다.
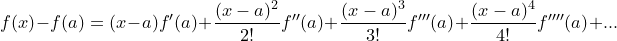
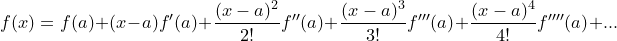
식이 너무 길기 때문에 우변을 합으로 나타내면
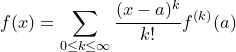
아래와 같은 식이 완성됩니다.
활용하기
특정 함수에 테일러 급수 전개를 해보고 이를 파이썬으로 직접 구해 봅시다.
파이썬을 사용하는 이유는 세밀한 연산을 위한 소수점 범위를 직접 지정할 수 있는 Decimal 모듈과 long long범위 이상의 계산을 지원하기 때문입니다.
sin(x)
풀이
sin(x)을 3차 미분까지 진행한 값은 아래와 같습니다. 4차 미분부터는 계속 값이 반복됩니다.
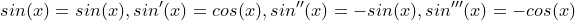
테일러 급수에 적용해 봅시다.
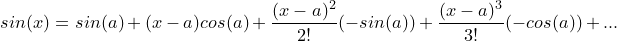
테일러 급수를 전개해도 우변에 삼각함수들이 남아있습니다. 이러면 사실상 테일러 급수를 활용하는 것 자체가 의미가 없어지게 됩니다. 삼각함수를 없애는 방법을 찾아야 합니다.
a값을 정하면 되는 데, 어느 각도에서도 적용이 가능하지만, 가능한 값이 무리수가 아니어야 좀 더 정확한 값을 측정할 수 있게 됩니다. a=0이면 sin0 = 0, cos0 = 1이 되므로 a=0을 대입합니다.

sin0=0이기 때문에 sin이 들어간 항은 전부 사라지고 cos만 남았습니다. 이 식도 합으로 표현하면
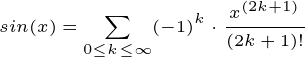
위와 같은 식이 완성됩니다.
코드
연산을 적게 해도 유사값이 바로 나타나기 때문에 Decimal을 사용하지 않았습니다.
PI = 3.14159265358979323846
def pow(r: float, n: int):
"""
O(logN) 자리 거듭제곱 함수
중요한게 아니므로 생략
"""
def sin(x: float, n: int):
res = 0
# 팩토리얼 계산
facts = [1] * (2*n+3)
for k in range(1, 2*n+3):
facts[k] = facts[k-1] * k
# 테일러 다항식 계산
for k in range(n+1):
res += pow(-1, k) * (pow(x, 2*k+1) / facts[2*k+1])
return res
if __name__ == '__main__':
print('==== sin(30) ====')
for i in range(0, 10):
print(f'{i}: {sin(PI/6, i)}')본래 테일러 급수에서는 무한번 까지 돌리게 명시를 해두었지만, 실제 컴퓨터에서는 무한대를 돌릴 수 없기 때문에 10번 정도만 돌리게 했습니다.
==== sin(30) ====
0: 0.5235987755982988
1: 0.49967417939436376
2: 0.5000021325887924
3: 0.4999999918690232
4: 0.5000000000202799
5: 0.4999999999999643
6: 0.5
7: 0.49999999999999994
8: 0.49999999999999994
9: 0.4999999999999999410번만 돌려도 근사값은 실제값과 거의 유사할 정도로 충분히 도출되는 군요. Decimal를 사용했다면 아마 훨씬 더 정밀한 값이 도출되지 않았을 까 싶습니다.
cos(x)
풀이
cos함수도 원리는 sin과 동일합니다. 4배수 미분한 값은 서로 동일하고 이를 테일러 급수에 적용하고 a=0로 세팅해 두면, sin이 있는 항은 없어지고 cos가 있는 항만 살아남습니다. 이때 cos가 있는 항은 sin과 다르게 홀수번째 항입니다.
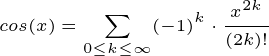
코드
PI = 3.14159265358979323846
def pow(r: float, n: int):
"""
O(logN) 자리 거듭제곱 함수
중요한게 아니므로 생략
"""
def cos(x: float, n: int):
res = 0
# 팩토리얼 계산
facts = [1] * (2*n+1)
for k in range(1, 2*n+1):
facts[k] = facts[k-1] * k
# 테일러 다항식 계산
for k in range(n+1):
res += pow(-1, k) * (pow(x, 2*k) / facts[2*k])
return res
if __name__ == '__main__':
print('====== cos(60) ======')
for i in range(0, 10):
print(f'{i}: {cos(PI/3, i)}')====== cos(60) ======
0: 1.0
1: 0.45168864438392464
2: 0.501796201500181
3: 0.4999645653289127
4: 0.500000433432915
5: 0.4999999963909432
6: 0.5000000000217777
7: 0.49999999999990047
8: 0.5000000000000004
9: 0.5000000000000001제곱근

위의 식을 테일러 급수에 적용해 봅시다.
풀이
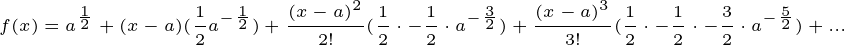
같은 미분값이 계속 반복되었던 sin/cos 함수와는 달리 제곱근의 경우 같은 미분값이 반복되지 않습니다. 하지만 일련의 규칙성을 찾을 수 있는 데, 우항으로 갈 수록 a의 지수값이 1씩 낮아지고 있고, 이전의 지수값들을 계속 곱하고 있습니다. a의 지수값들만 나열하면
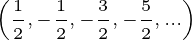
이 되고 이를 함수로 나타내면
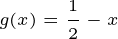
따라서 아까의 테일러 공식을 아래처럼 간단히 표현할 수 있습니다.
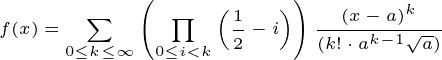
이제 a의 값을 정하기만 하면 됩니다.우변의 루트를 제거만 하면 되기 때문에 a값이 어떤 수의 제곱이기만 하면 됩니다. 4가 2의 제곱이므로 a=4를 대입해 봅니다.

이렇게 해서 제곱근에 대한 테일러 급수를 완성했습니다.
코드
from decimal import Decimal, getcontext
getcontext().prec = 50
def pow(r: Decimal, n: int):
# 거듭제곱
if n == 0:
return Decimal(1)
elif n == 1:
return r
else:
half = pow(r, n>>1)
v = half * half
if n%2 == 0:
return v
else:
return v * r
def sqrt(x: float, n: int):
res = Decimal(2)
x = Decimal(str(x))
# g(x) = 1/2 - (x-1)에 대한 합 계산
sum_g = [Decimal(0)] * (n+1)
sum_g[1] = Decimal(0.5)
for k in range(2, n+1):
sum_g[k] = sum_g[k-1] * (Decimal(1/2) - (k - 1))
# 팩토리얼 계산
facts = [Decimal(0)] * (n+1)
facts[0] = facts[1] = 1
for k in range(2, n+1):
facts[k] = facts[k-1] * k
# 테일러 다항식 계산
for k in range(1, n+1):
res += (sum_g[k] * (pow(x-4, k)/(facts[k] * pow(2, 2*k-1))))
return res
if __name__ == '__main__':
# 루트 2 구하기
root2 = Decimal(0)
i = 1
while True:
res = sqrt(2, i)
if root2 == res:
break
root2 = res
i += 1
print('루트2: ', i, root2)
# 루트 3 구하기
root3 = Decimal(0)
i = 1
while True:
res = sqrt(3, i)
if root3 == res:
break
root3 = res
i += 1
print('루트3: ', i, root3)이번엔 Decimal 모듈을 사용했고 소수점 50자리 까지 설정했습니다.
루트2: 153 1.4142135623730950488016887242096980785696718753769
루트3: 77 1.7320508075688772935274463415058723669428052538105루트2인 경우, 153번 까지 미분을 해서 50자리 근사값을 구했고, 루트3인 경우 77번 까지 미분을 해서 구했습니다. 이 값들은 실제 루트 값의 50자리 까지 일치합니다.
끗
이렇게 해서 테일러 급수에 대한 첫 번째 리뷰를 마쳤습니다. 제곱, 세제곱근이나 삼각함수같은 주요 함수들은 각 프로그래밍 언어 자체에 내장되어 있지만, 정밀한 계산을 요구할 때 테일러 급수를 이용해서 정밀한 근사값을 구할 수 있습니다.하지만 그만큼 시간이 오래 걸리게 됩니다. 예를 들어 아까 위에 루트2의 근사값을 구할 때 까지 153번을 반복했습니다.
하지만 어디까지나 근사값을 구하기 때문에 항싱 실제 값과 당연히 오차가 생길 수 밖에 없습니다. 다음 챕터에서는 테일러 다항식의 개념과 테일러 다항식의 상대/절대 오차에 대해 리뷰할 예정입니다.
놀랍게도 테일러 급수와 관련된 코딩문제가 있다
13705번: Ax+Bsin(x)=C
첫째 줄에 정수 A, B, C가 주어진다. (0 < B ≤ A ≤ 100,000, 0 < C ≤ 100,000)
www.acmicpc.net
방정식에 대한 해를 찾는 문제 입니다. 소숫점 여섯째 짜리 까지만 출력하라고 명시되어 있지만 스페셜 저지가 없는 것으로 보아 상당히 정밀한 값을 요구하고 있습니다. 일반 sin함수로는 한계가 있기 때문에 테일러 급수를 이용해 문제를 풀어야 합니다. 파이썬으로 푸는 것을 권장합니다. (티어가 너무 높은 관계로 솔루션 코드는 공개하지 않습니다.)
(부록) 주요 테일러 급수 리스트
출처: 위키백과
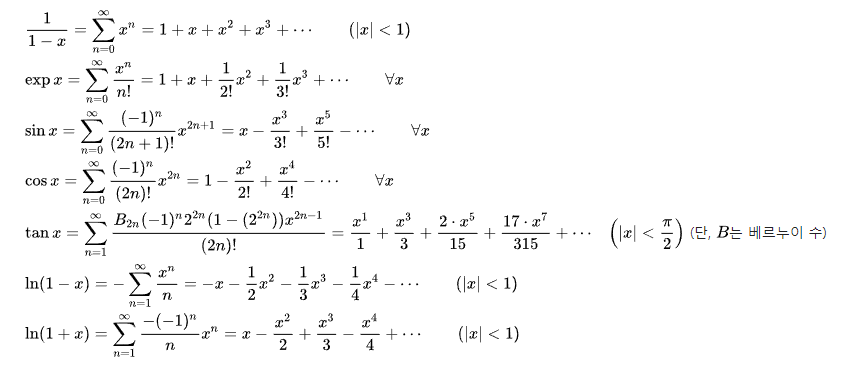
'수학 관련 > 수치해석' 카테고리의 다른 글
| [수치해석] 테일러 급수 (2) - 테일러 다항식과 테일러 다항식의 오차 구하기 (0) | 2022.07.14 |
|---|---|
| [수치해석] 가우스 소거법으로 연립방정식을 풀어보자 (0) | 2022.07.04 |



