| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 취업
- 이분 탐색
- 백엔드
- 개발자
- alembic
- 리트코드
- BFS
- sqlalchemy
- api서버
- 웹서버
- 수학
- 구성적
- 백준
- MYSQL
- SQL
- 아파치
- 테일러 급수
- scc
- 위상 정렬
- C언어
- 알고리즘
- 데이터베이스
- 신입
- FastAPI
- python
- 강한 연결 요소
- Django
- flask
- 가우스 소거법
- 파이썬
- Today
- Total
Devlog
[알고리즘] 강한 연결 요소(1): 코사라주 알고리즘 본문
강한 연결 요소 (Strongly Connected Component) 시리즈
1. 코사라주 알고리즘
2. 타잔 알고리즘
3. 2-SAT

소개
강한 연결 요소(Strongly Connectioned Component)는 그렇게 잘 알려져 있는 알고리즘이 아니지만 제법 유용하게 쓰일 수 있는 알고리즘 입니다. 그래프에서 정점들 중 일부분이 서로 도달할 수 있는 정점들의 집합을 강하계 연결되었다. 라고 합니다. 강한 연결 요소 알고리즘이란 강하게 연결되어 있는 정점들의 집합의 정보를 구하는 알고리즘 입니다.
크게 코사라주 알고리즘과 타잔 알고리즘이 있습니다. 코사라주 알고리즘이 구현 난이도가 쉽기 때문에 이번 챕터에서는 코사라주 알고리즘 부터 설명합니다.
알고리즘 작동 방식
코사라주 알고리즘의 그래프이 간선 방향이 달라도 강한 연결 요소는 일치함을 이용해서 요소들을 찾습니다. 그렇기 때문에 DFS를 정방향 한번, 역방향 한번 해서 총 두번 돌립니다. 알고리즘 순서는 다음과 같습니다
- 전체 정점에 대해 DFS를 수행합니다. 이때 DFS를 통해 저장될 정보는 처음으로 탐색된 순서가 아닌 탐색을 마친 순서 입니다.
- 다시 정점에 대해 역방향 DFS를 수행합니다. 이때 정방향 DFS에서 얻은 리스트(탐색을 마친 순서)에서 맨 마지막에 탐색을 마친 순서 부터 차례대로 DFS를 수행합니다. 한 번 DFS를 수행하고 난 후의 탐색된 정점들은 하나의 강한 연결 요소가 됩니다.
1번에서 설명된 탐색을 마친 순서는 이진 트리 탐색에서의 후위 순회와 매커니즘이 비슷하다고 보시면 됩니다. 말 그대로 해당 정점으로부터 이어져 있는 모든 정점들을 탐색하고 난 후의의 시점을 의미합니다.
def dfs(u):
for v in graph[u]:
if visited[v]:
continue
visited[v] = True
dfs(v)
# 하위 정점들을 모두 탐색한 후 완료 리스트에 추가한다.
finished.append(u)예제 문제와 코드 (Python)
2150번: Strongly Connected Component
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정
www.acmicpc.net
주어진 그래프에 강한 연결 요소를 찾고 그 내용을 출력하는 문제 입니다. 우선 입력이 들어오면 정방향 그래프와 역방향 그래프를 생성합니다.
# 입력
for _ in range(E):
u, v = map(int, input()[:-1].split())
graph[u].append(v)
rev_graph[v].append(u)그 다음 정방향 DFS를 사용해서 후위 탐색 순서를 구합니다. 이때 모든 정점을 상대로 DFS를 수행합니다.
# 정방향 DFS
def dfs(u):
for v in graph[u]:
if not visited[v]:
visited[v] = True
dfs(v)
finished.append(u)
# 정방향 DFS 수행
for start in range(1, V+1):
if not visited[start]:
visited[start] = True
dfs(start)마지막으로 역방향 DFS를 수행합니다. 노드 순서는 finished의 역방향이며 한 번 DFS해서 나온 정점들은 하나의 강한 연결 요소가 됩니다.
# 역방향 DFS
def rev_dfs(u, elements):
elements.append(u)
for v in rev_graph[u]:
if not visited[v]:
visited[v] = True
rev_dfs(v, elements)
# visited 초기화
visited = [False] * (V+1) # 방문 여부
# 마지막에 탐색이 완료된 정점 순으로 역방향 DFS
ans = []
while finished:
start = finished.pop()
if not visited[start]:
elements = []
visited[start] = True
rev_dfs(start, elements)
ans.append(elements)전체 코드 (Python)
import sys
import collections
sys.setrecursionlimit(10**6)
# Inputs
input = sys.stdin.readline
V, E = map(int, input()[:-1].split())
graph = [[] for _ in range(V+1)] # 정방향 그래프
rev_graph = [[] for _ in range(V+1)] # 역방향 그래프
visited = [False] * (V+1) # 방문 여부
finished = [] # 먼저 방문을 마친 순서
# 입력
for _ in range(E):
u, v = map(int, input()[:-1].split())
graph[u].append(v)
rev_graph[v].append(u)
# 정방향 DFS
def dfs(u):
for v in graph[u]:
if not visited[v]:
visited[v] = True
dfs(v)
finished.append(u)
# 역방향 DFS
def rev_dfs(u, elements):
elements.append(u)
for v in rev_graph[u]:
if not visited[v]:
visited[v] = True
rev_dfs(v, elements)
# 정방향 DFS 수행
for start in range(1, V+1):
if not visited[start]:
visited[start] = True
dfs(start)
# visited 초기화
visited = [False] * (V+1) # 방문 여부
# 마지막에 탐색이 완료된 정점 순으로 역방향 DFS
ans = []
while finished:
start = finished.pop()
if not visited[start]:
elements = []
visited[start] = True
rev_dfs(start, elements)
ans.append(elements)
# 출력
for k in range(len(ans)):
ans[k].sort()
ans.sort(key=lambda e: e[0])
print(len(ans))
for k in range(len(ans)):
ans[k].append(-1)
print(*ans[k])근데 원리가 뭐지?
이렇게 보니 일단 알고리즘 자체는 쉬운 것 같습니다. DFS 단순히 두 번만 돌리면 되니깐요. 그런데 문제는 원리가 무엇이냐 입니다. 비록 위에 간선 방향이 달라도 요소는 일치하다 라고는 적어뒀지만, 왜 역방향 탐색을 할 때 왜 후위 탐색의 역순서로 진행하는 지에 대해 충분한 설명이 되지 않는 것 같습니다.
보조 정리1
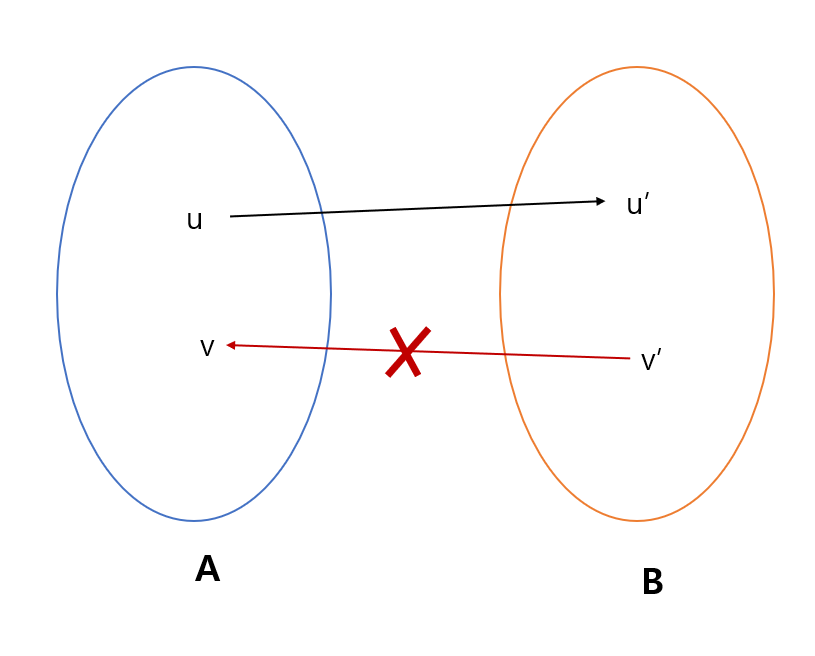
어느 한 그래프에서 서로 다른 강한 연결 요소 A와 B가 있다고 가정하자, 그리고 정점 u,v가 A에 속하고, u'.v'가 B에 속한다고 하자, 그리고 간선 (u, u')(또는 u->u')가 있다고 할 때, (v',v)인 간선은 존재하지 않는다.
귀류법으로 증명할 수 있습니다. 만약 (v', v)이라는 간선이 존재한다고 가정을 합니다.
일단 (u, u')가 존재한다고 했으니, v -> u -> u' -> v'라는 간선도 존재합니다. 그런데 (v', v)의 간선 까지 존재하게 되면 v -> u -> u' -> v' -> v 순으로 v로 다시 되돌아 오므로 하나의 강한 연결 요소가 되지만. 위의 정의에서 A, B는 서로 다른 강한 연결 요소 이므로 서로 모순이 되기 때문에 (v', v)라는 간선은 존재하지 않습니다.
보조 정리2
그래프 상에서의 서로 다른 연결 요소 A, B가 있고, 정점 u는 A에 속하고, 정점 v는 B에 속하며 (u, v)라는 간선이 존재할 때, 탐색 종료 시간은 B보다 A가 더 늦다.
정리에 대한 증명을 하기 전에 아래와 같은 함수를 정의합니다.
d(x): DFS 탐색 중에 x의 탐색이 시작되는 시간. x가 정점아닌 요소일 경우, 처음 x에 속하는 정점을 탐색하는 시간이 된다.
f(x): DFS 탐색 중에 x의 탐색이 끝나는 시간. x가 정점 아닌 요소일 경우, 모든 요소 x의 정점의 탐색이 끝나는 시간이 된다.
그렇다면 보조 정리2 의 명제를 정리하면 u ∈ A, v ∈ B이고 (u, v)가 있을 때, f(A) > f(B)가 된다. 라고 정리할 수 있습니다.
근데 사실 이걸 증명하는 방법도 쉬워 보입니다. a -> b 방향의 그래프가 있다고 가정할 때 a부터 탐색을 시작해서 b로 가는 데, 탐색 시작 순서는 a -> b이지만 탐색이 끝나는 순서는 b -> a이기 때문에 f(b) < f(a)가 됩니다.
위의 명제도 마찬가지로 DFS를 탐색하다가 A를 만났을 경우, A의 정점을 일부분 순회하다 u -> v를 만나게 되고 중간에 B를 전부 순회한 다음 A로 돌아와서 마저 순회하게 됩니다. 순회 순서를 식으로 정리하면 A -> B -> A가 되고, 탐색 종료 순서는 B -> A가 됩니다. 그러므로 f(A) > f(B)가 맞게 됩니다.
그런데 문제는 그 반대의 경우 즉, A가 아닌 B가 발견되는 경우 입니다. B가 먼저 발견되었다고 가정합니다. 하지만 B는 순회하면서 도중에 A로 가지 않고, B를 전부 돌다가 끝나게 됩니다. 그 이유는 u -> v만 있지 v -> u로 가는 방향은 존재하지 않기 때문에 A로 넘아갈 방법이 없습니다. (v -> u 가 존재하면 사실상 하나의 요소가 되는데 보조 정리1에 따라 서로 다른 A, B이기 때문에 모순이 됩니다.)
따라서 B를 탐색해서 B를 종료한 다음, A를 탐색해서 A를 종료합니다. 탐색 종료 순서는 B -> A가 되므로 f(A) > f(B)가 됩니다.
따름 정리
G(t)를 역방향 그래프 라고 정의하고 E(t)를 역방향 그래프에서의 간선의 집합이라고 정의한다.
f'와 g'는 f와 g의 역방향 탐색 시작/종료 시간이라고 정의한다.
G에서의 강한 연결 요소 A, B가 있고, G의 정점 u, v가 있을 때, u ∈ A, v ∈ B 이며 (u, v)가 E(t)에 있다고 할 때 f(A) < f(B) 이다.
E(t)에서 (u, v)가 있다고 하면 정방향인 E에서는 (v, u)가 존재합니다. 간선이 B -> A로 이동하는 간선이 존재합니다. 따라서 보조 정리 2에 의해 f(A) < f(B)가 맞습니다.
당연한 거지만 이 정리는 보조 정리2와 같이 활용하면 두번 째 역방향 DFS 탐색에서 무슨 일이 일어나는 지를 짐작할 수 있습니다.
최종 증명
아까 보조 정리 2에 의하면 B -> A 방향이기 때문에 처음 정방향 DFS를 수행했을 때, f(B) > f(A)가 됩니다. 물론 탐색 도중에 A와 B사이를 왔다갔다 할 수 있겠지만, f(x)에서 x가 정점 아닌 모든 요소들의 탐색이 완료되는 시점이므로 해당 명제가 맞습니다.
그렇다면 두 번 재 역방향 DFS를 수행할 때 정점의 순서는 맨 마지막으로 탐색이 완료된 정점 순으로 하게 되고, B에 속하는 정점 탐색부터 시작하게 됩니다. 이때 역방향 상에서의 간선은 A -> B가 되고 탐색 종료 순서는 B -> A순서 입니다.
정방향에서는 B -> A -> B -> ... -> A로 중간에 왔다갔다 하는 경우가 있지만. 역방향의 경우 B -> A로 가는 간선이 없습니다. 따라서 B의 모든 정점을 탐색할 때 까지는 다른 영역의 정점을 탐색하지 않게 되고 B에서의 DFS가 끝나면 B에 속하는 정점들만 리스트로 출력하게 됩니다. 이를 모든 정점을 탐색할 때 까지 반복하면 강한 연결 요소들을 찾을 수 있게 됩니다.
반례로 역방향 그래프 상에서의 B -> A도 존재하게 된다면 역방향과 정방향 모두 A -> B, B -> A로 가는 간선이 존재하고, 이는 보조 정리1에 의해 모순이 됩니다.
마치며
코사라주 알고리즘은 DFS만 두번 돌리면 끝이기 때문에 구현 난이도는 상당히 쉽습니다. 하지만 적용이 어렵기 때문에 실제로는 타잔 알고리즘을 많이 사용합니다. (실제로 SCC를 구글링 해보면 대부분 코사라주 보다는 타잔 알고리즘을 설명하는 경우가 더 많습니다.) 다음 챕터에서는 타잔 알고리즘에 대해서 설명할 예정입니다.
'Problem Solving > 알고리즘' 카테고리의 다른 글
| [알고리즘] 이분 탐색의 변종들 (1) - lower/upper bound를 알아보자 (0) | 2023.03.26 |
|---|---|
| [알고리즘] 강한 연결 요소(2): 타잔 알고리즘 (8) | 2022.07.02 |
| [알고리즘] 위상 정렬 (정리) (0) | 2022.05.19 |


